I know, I know. After the 2012-2017 Great Equivalence War, photographers everywhere agreed never to utter that word again. Nasim’s famous quote, “Everyone is right, everyone is wrong,” has been etched both into the peace treaty and into the hearts of millions. However, as we near the two-year anniversary of the ceasefire, it seems that isolationist thoughts – i.e., that equivalence is isolated just to focal length – are resurfacing again. Let’s stop this madness before it’s too late.
Note: On Photography Life, we already have a very detailed article on equivalence here. It goes into things like print size, pixel density, diffraction, and the ugly duckling of “total light.” Feel free to read it if you’re interested in those topics. The article below is limited in scope simply to focal length, aperture, and ISO – the three key takeaways from the equivalence discussion that I think everyone should know.
That’s my true reason for writing this article: to emphasize the three important takeaways of equivalence. Quite simply, now that we’ve entered a bit of a cool-down period on the equivalence debate, it’s become a good time to turn back and examine it with rational heads. There are useful things to be gained from equivalence. It directly matters any time you try to recreate the look of a particular image (such as an inspiring portrait photo you saw online), or when you’re deciding among camera systems in the first place.
Table of Contents
A Quick Refresher
Before we start, what is equivalence? Quite simply, it’s the way you can take similar looking photos with two different cameras – two cameras of differing sensor sizes, to be more specific.
If you want to take equivalent photos with a Nikon DX crop-sensor camera and a Nikon FX full-frame camera, you’ll need to do a few calculations. (They aren’t hard, and I’ll cover them below.) Sure, a thousand little differences mean that your photos will never look identical even after you get the math right. But when you get down to the essence of equivalence, that’s all superfluous. Instead, you’re left with only three variables still standing: focal length, aperture, and ISO.
Don’t Move
All of equivalence – all of it – assumes that you don’t move your physical position. Equivalence goes completely out the window once you start moving. That’s because any time you move, you change the relative sizes of objects in your photo. This is called perspective, and it’s a cruel force if equivalence is your goal; with different perspectives, it just isn’t possible to capture two identical photos. So, the entire discussion below assumes that you’re standing still, because otherwise you might as well be reading a completely different article (like Elizabeth’s on lens compression).
Why Focal Length Is Clearly Part of Equivalence
A crop sensor is exactly like a crop from a large sensor. Put a 1.5x crop camera next to a full-frame camera in 1.5x mode, and the photos will be identical. (Naturally, assume the same lens, sensor megapixels, pixel-level performance, aspect ratio, people jumping in front of the camera, and the camera’s mood that day. Also assume that this is the only such disclaimer I’ve included in the article, so feel free to repeat it aloud as needed below.)
As you almost certainly know, you need to use a longer lens on the full-frame camera to match the crop camera. It’s the only way to match the fields of view between the images. (I know it’s hardly been a paragraph, but my foot is starting to twitch, so I’ll break my no-disclaimer rule just once to say okay, unless you crop or stitch a panorama.)
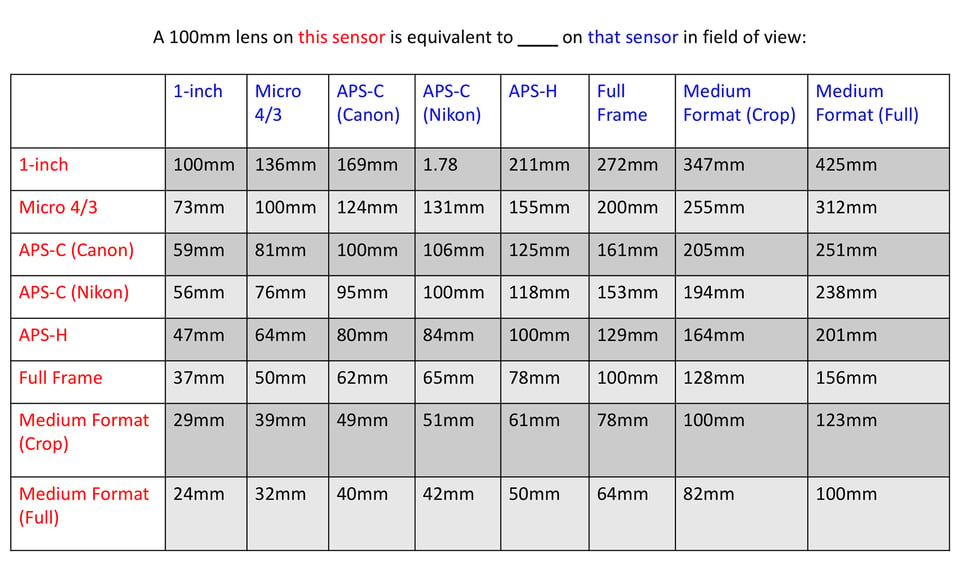
The formula for equivalent focal length is easy: (focal length) x (crop factor). For example, a 100mm lens on a 1.5x camera is like a 150mm lens on full-frame camera, at least for field of view. Hopefully this fact is already second nature to you.
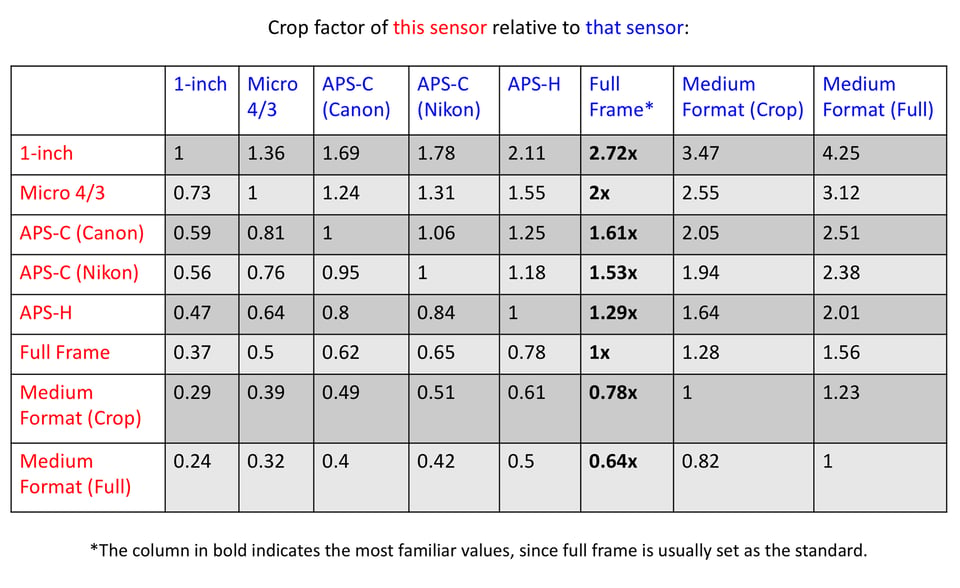
Things get a bit more complicated – though not much – if neither camera in question is full frame, just because math like “1.5x crop” is assumed to be relative to full frame. For example, say that you’re trying to calculate equivalence between an APS-C and medium format camera. In this case, you need to look at the ratio of their sensor diagonals to find the crop factor between the two.
It’s not the easiest thing to understand in paragraph form, so I created two color-coded tables below to make things easier to visualize. The first chart simply shows crop factors:
While the second chart shows you the equivalent of a 100mm lens on your camera:
All right. Everyone agrees that focal length is part of equivalence. I’ll add a couple sample photos below, even though hopefully I don’t need to. Click to view full screen and switch from one to the next:
A lot of photographers stop here, but that’s not good. As you can see in the images above, even though the fields of view are identical, depth of field is not (which will be more visible in the next section’s photos). That’s because aperture is also part of equivalence – and so is ISO.
Aperture and Equivalence
Before I go into any details, let me simply mention one thing: the formula for equivalent aperture is exactly the same as the formula for equivalent focal length. Just do (f-number) x (crop factor). To take equivalent photos, you’ll be at f/4 on a 1.5x sensor alongside f/6 on a full-frame sensor.
While I’m at it, I’ll mention another thing: right now, I’m only talking about depth of field. If you don’t also do the next step (the ISO side of things), the f/6 photo will be significantly darker than the f/4 photo. And this only applies when your fields of view are matched already – after you’ve zoomed in with the larger sensor.
See, the aperture side of equivalence is actually about fixing a problem you made a moment ago. When you zoom in at a constant aperture, depth of field decreases. A 200mm photo does not have the same depth of field as a cropped 100mm photo. If you don’t believe me, here’s the proof:
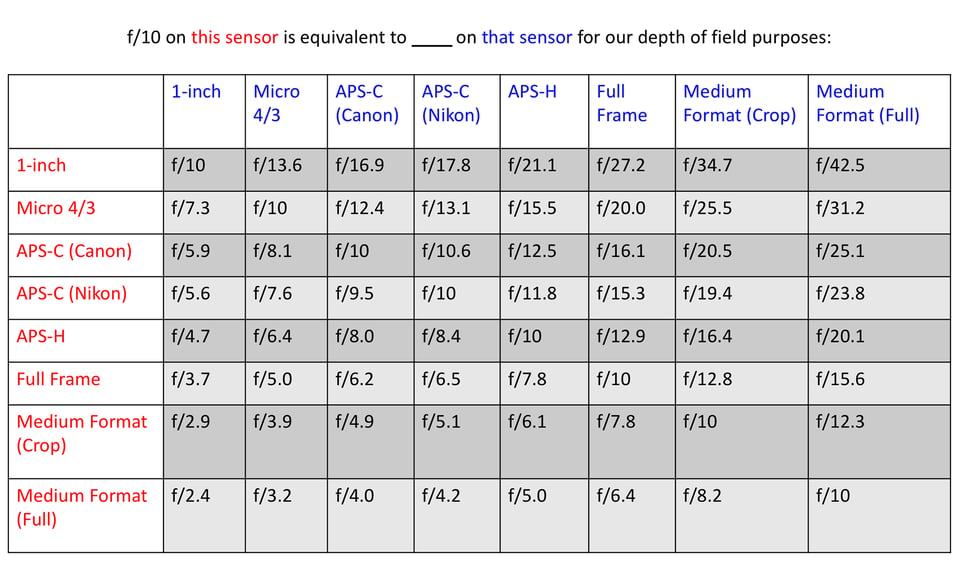
Clearly, the first image has a shallower depth of field. So, when you crop your photos by using a crop-sensor camera, you need to do something about the depth of field problem. Otherwise, you just can’t get equivalent images. As I said a moment ago, the exact fix is (f-number) x (crop factor).
Because the example photo above simulates a 2x crop factor, that’s simply f/8. So, we can expect that f/8 at 200mm provides similar depth of field as f/4 at 100mm, cropped to match the field of view. And it does. The following image, taken at f/8, has the same depth of field as the prior one:
This formula applies just as well for “stranger” cases of equivalence, too, like the APS-C vs medium format example above. So, here is the same chart from earlier, but for an example aperture of f/10:
ISO and Equivalence
You now have two photos from different camera sensors, yet you’ve managed to capture the same field of view and the same depth of field – not bad. At this point, the obvious difference is that one photo is darker than the other. Specifically, the larger-sensor camera is now capturing underexposed images, which is no surprise, since you decided to use a smaller aperture on it. What were you thinking?
Clearly, you were thinking that you can just raise the ISO on the large sensor camera to compensate. Most likely, it already has better high ISO performance than the crop sensor, so it works out to be roughly an even trade. And you’re quite right to think that!
In fact, let’s revisit the 2x crop sensor example. Your apertures in this case are f/4 and f/8, as I showed a moment ago. That’s two stops of difference. And, by actual magic (AKA physics), full-frame sensors are about two stops better in high ISO performance than 2x crop cameras.
On 1.5x APS-C sensors, that’s f/4 and f/6, roughly 1.3 stops of difference. Who would have guessed? Full-frame sensors are about 1.3 stops better than APS-C sensors at high ISOs. Also by magic.
On the rare 1.3x APS-H Canon cameras, that’s f/4 and f/5.2, a little less than one stop of difference. Hopefully, it’s no surprise to hear that Canon’s APS-H cameras performed about one stop worse at high ISOs versus the company’s same-generation full-frame cameras.
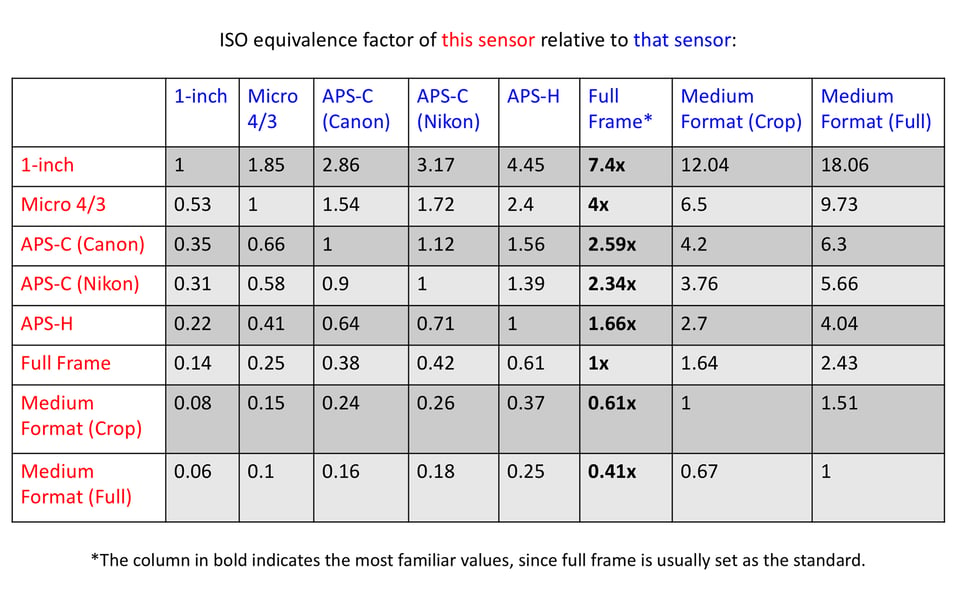
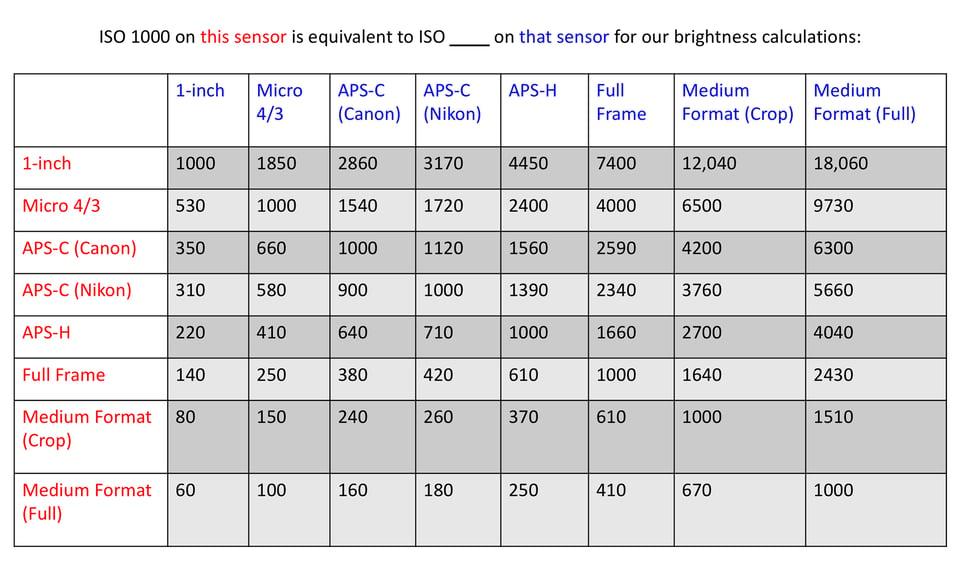
So, what’s the underlying formula here? It’s similar to the first two, although slightly more complicated. In order to factor ISO into equivalence – thus fixing differences in brightness and noise performance – the equation is: (ISO) x (crop factor^2).
As you can see, you need to square your crop factor first. For example, this leads to equivalence between f/4 and ISO 1000 (on a 2x crop camera) compared to f/8 and ISO 4000 (full-frame). Or f/4 and ISO 1000 (1.5x crop camera) versus f/6 and ISO 2250 (full-frame). You get the point.
Here are the tables demonstrating how this applies in practice:
And then a chart at ISO 1000:
And the holy grail you’ve been waiting for – two photos taken with different camera sensor sizes, yet an equivalent appearance:
The ideal settings would have been f/5.2 and ISO 1367, but those aren’t values that the D7000 can set. Instead, the closest approximation was f/5 and ISO 1250, which is still similar enough that the photos look equivalent.
That also holds up at pixel level, as you can see in the following 100% crops (after downsampling the D800e image to match the D7000):
Noise levels are pretty much the same. Small differences aren’t a surprise – and there are a few here – but overall these photos are as equivalent as they can be.
Sometimes, Equivalence Isn’t Possible with Your Gear
There’s a reason why photographers pay top dollar for lenses like the Canon 50mm f/1.2 or Sigma 14mm f/1.8 with a full-frame camera. Companies simply don’t make 35mm f/0.8 or 9mm f/1.2 lenses for APS-C crop sensor cameras, which is what it would take to achieve equivalence.
Even if those lenses did exist, most crop-sensor cameras still lack ultra-low ISO values. So, if your large sensor is at base ISO, you probably can’t do the ISO part of equivalence; the small sensor simply can’t go low enough to compensate. Instead, you’ll have to set it to base ISO as well, and darken the photo as needed with a faster shutter speed. That makes the photos look equivalent at a broad level (field of view, depth of field, and brightness). But since you’re at base ISO on both cameras, the large sensor is likely going to win in terms of things like dynamic range and color depth.
As a side note, smartphone manufacturers have tried to get around this by using a low base ISO of around 25 on many models. However, standard smartphones have tiny sensors with a 7x crop factor versus full-frame. That leads to an equivalent ISO of 25 x 7^2, or about ISO 1250. Next time you wonder how much image quality you give up with a phone, remember that the best case is like shooting all your DSLR images at ISO 1250.
Other times, equivalence works in your favor, and there is no theoretical difference between a small sensor or large sensor for the photo you want:
Print Size, Total Light, Airy Disks, Circles of Confusion, and Eigenvalues
Just kidding.
Conclusion
Equivalence is among the nitty-grittiest of the nitty-gritty. There are so many details that can change the discussion wildly, especially if your camera sensors don’t have the same pixel-level performance (which is pretty much all sensors). The best you can do is get the theory right – the math in this article – and accept that image quality differences are going to remain based on your sensor itself. Just to refresh, that math is as follows:
- Equivalent Focal Length = (Focal Length) x (Crop Factor)
- Equivalent Aperture = (F-Number) x (Crop Factor)
- Equivalent ISO = (ISO) x (Crop Factor^2)
You need to apply all three in order to get an equivalent photo. Don’t misinterpret that I’m saying “ISO 200 on M4/3 is the same as ISO 800 on full frame.” It’s not. Hopefully this goes without saying, but any side-by-side test will show ISO 800 to be brighter than ISO 200. However, if you want equivalent photos on both these cameras, you’ll need to shoot your full-frame sensor at twice the focal length, twice the f-number, and four times the ISO.
To me, that’s the takeaway that matters in the equivalence discussion. You can debate all day about sensor efficiencies, lens T-stops, X-Trans vs Bayer, CCD vs CMOS, and a million other things. But if you don’t at least take into account focal length, aperture, and ISO, you’ll never get equivalent photos across different camera systems.
I do want to emphasize that equivalence is rarely something you’ll need to think about in the field – but it does matter a lot in certain non-field cases. If you see an amazing photo and wonder how to get the same look in your images, just do some quick calculations to figure out the right settings. Or, if you’re deciding between two camera systems, it helps to know exactly what you’re giving up with one versus the other.
On top of that, I believe that learning the advanced technical side of photography makes it easier to internalize the basics, something that directly impacts the quality of your photos. I also don’t want photographers to waste their time in forum arguments if there is any way around it. Hopefully, a math-based understanding of equivalence, especially the main takeaways, will help you avoid that fate – or, if it’s doomed to happen either way, at least dominate the discussion boards and prove to everyone that you’re the Best Photographer™.
Spencer,
First, thanks for an excellent article. The clarity of the piece really focuses on what I need to know.
Second, the article corrected a misunderstanding I had about the relevancy of the equivalency concept to aperture size. Further I had not understood that there is an equivalency concept applicable to ISO.
Now the question. If a full frame camera and full frame lens are setup to provide an equivalent field of view offered by an APC camera (Nikon) and APC lens combo, why does the latter combo supposedly provide a greater magnification of the image? Is there some equivalency formula for magnification of the image?
Well done! Another twist in the calculation is pixel density among sensors. I think the math is accurate for ISO when comparing a 24mp full frame vs a 24mp APS-C sensor but may not be if the the full frame is 61mp vs 24mp on the APS-C. In that case they’re probably about equal ISO. Anyway it’s a very arguable subject which you did a great job explaining.
Actually the math is the same but you have to consider multiple factors. The effective ISO and relative noise is near the same between 24 MP full frame and 61 MP full frame (with a slight advantage to the 24 MP camera). The 61MP camera has smaller photosites resulting in a little more noise, but it also has the benefit of downsizing to a common output with the same size sensor. Downsizing from 61MP to 24 MP or a common print size picks up roughly 1 stop of benefit. You can see this on Photonstophotos.net.
If you were cropping to the same size – 24 MP – you would also lose the benefit of downsizing. At PhotonstoPhotos you can see that a DX crop has about 1 stop less photographic dynamic range than a full frame, uncropped image with the same camera. APS-C cameras have a smaller sensor so in relative terms, it’s the same as cropping the image from a full frame camera.
Over the past 8 years there is very little difference in the technology, and no difference in the underlying physics. Photontophotos.net includes Ideal FX and Ideal DX in their list of cameras so you can see we are pretty close to theoretical maximums unless you introduce types of processing and noise reduction to the RAW file such as dual gain.
Eric, you’re absolutely right. On 24 MP sensors, our tests generally show less than 1 stop of noise improvement at very high ISOs compared to 45 or 63 MP. This is after downsampling the higher-res image to 24 MP.
And I’m glad to hear that there has been no difference in the underlying physics since I wrote this article! I would be a tad concerned otherwise :)
Well written
Considering sensors of the same size, same gen, and by the same manufacturer can vary wildly based on configuration, this is purely just bad advice. If someone is going from a Canon FF to a Fuji APS-C, this will not be accurate. In general sensor size has nothing directly to do with exposure outside of having more flexibility on how it’s configured. You can really only make an equivalency chart for a specific camera/sensor combo and another camera sensor combo. It’s as simple as that, this is just pseudo science that realities disprove. If you go by this bad advice you’ll have all kinds of varying results.
If this article is so wrong that you felt the need to reply to half the comments and trashing it, how did I use this information to get the equivalent sample images you see in the article?
You’re obviously right that there are individual sensor differences which still matter from camera to camera. For example, you cannot expect that a Sigma Foveon sensor optimized for color detail at base ISO would be a match for some amazing Fuji sensor at high ISOs, even with the same sensor size.
I literally said as much in the article: “Naturally, assume the same lens, sensor megapixels, pixel-level performance, aspect ratio, etc…”
The key that you seem to be deliberately overlooking is that the math in this article is the conceptual basis that underpins things – upon which individual sensor or lens differences can shift results. If you think that’s wrong, point me to one incorrect sentence in this article. As always, if I made any technical mistakes, I will correct them and admit my error.
Isaac Ah-Loe…Article really confused me…maybe you can help with all this equivalency, F stop specifically. I have read that to achieve the same dof on an apsc (Fuji XT3) landscape images, you should open up one stop. So normally I look at a scene and say I want to shoot at F16 as that will give me the results I want (~3 feet to infinity in focus) Lens 16-55 mm shot at 16mm. So on an apsc I would shoot at F11….correct??
From the article….but lens are not equivalent
Picture Taken at 14mm f/2.8 on a full-frame sensor. For equivalent photos on an APS-C sensor (1.5x to 1.6x crop), you would need a 9mm f/1.8 lens, which currently does not exist.
Other times, equivalence works in your favor, and there is no theoretical difference between a small sensor or large sensor for the photo you want:
But why even be concerned about equivalency. All I care about is correct dof for a given scene….shoot at f11-f16 for dof from approx 3 feet (focus point) to infinity. Lens Fuji 16-55.
thanks
Okay so in order to capture the same image looking at the ISO charts a micro four thirds sensor capturing the image at ISO 100, would using these same equivalents require a full frame camera to use ISO 400.
Now if you were to use ISO 400 for this same image on the micro four thirds sensor it would be over exposed. In other words it would have captured too much light.
Yet everyone states the full frame captures more light?
Could it simply be that the acclaimed Bokeh of full framed cameras is down to their poor ability to capture light in any area not in focus?
You just got it all wrong pal
Thanks for the explanation. RE crop factors on the medium format sensors, what dimensions are you assuming for each?
OK, I know I’m commenting on an old thread . . . but, with so many reactions focusing on some arcane detail or simply concluding that all of this is irrelevant, I thought I’d share one practical use for me. I often like to shoot with two cameras, and ideally that would be two full frame bodies with fast zooms, 24-70 f/2.8 and 70-200 f/2.8. However, my “second” camera, APS-C and mirrorless, was chosen to be my primary camera when I want small and light (e.g., travel). So, in two-camera mode I would mount a 16-35 f/2.8 on the crop sensor body to get 26-56 focal length equivalent. For me, this was better than putting the 24-70 on crop since 26 is decently wide, and I don’t really care about the gap between 56 and 70. So far so good. But wait, that 16-35 f/2.8 “looks” like f/4.5 on crop. The solution for me was the Sigma 18-35 f/1.8 APS-C lens. That frames and looks like 29-56 f/2.9. Nice! Doesn’t hurt that it’s also an awesome lens–way better than the old 16-35 f/2.8 I’d been using.
OK, I’ll admit that these days I do have 2 full frame bodies that I could use, but I’m so pleased with the performance of the crop sensor lens at f/1.8 that I have no interest in carrying the weight of a second full frame with 24-70. Besides, my aging 24-70 is not nearly as sharp as the Sigma and upgrading it (full frame dollars) would cost way more than the APS-C lens did. The Sigma f/1.8 APS-C zooms are genius, not because they “let in more light” but because they allow APS-C shooters to achieve an equivalent look to full frame fast zooms.
Thank you for the great insight. I am confused about one thing…and this may be a bit unorthodox.
If I use a medium format lens on a camera with a 1″ sensor, the aperture is tiny (less than 1)?
The practical use case would be to put a Pentax 67 300 F4 lens on an adapted Nikon 1 J5 camera for astrophotography. Relatively speaking, it would be a super-fast lens with a long zoom. Am I missing something obvious?
Hi Thanks. My understand is as follows which is slightly different , I am wrong?
1) You change the focal length by the crop factor. Fine to get same field of view.
2) You change the f stop to by smaller (dividing by the crop factor) on the smaller sensor to get same depth of field . Fine.
3) So in you example you now have 200mm f8 (full frame) and 100mm f4 on sensor with a crop factor of 2
4) But the reason you need to increase ISO on the full frame sensor to get the same picture brightness I suggest is not because the f stop numbers are different as you suggest as lens aperture=focal length/f-stop number so the aperture diameter letting in light to each sensor is the same in both cases ie 200/8=100/4 or 25mm. Therefore the amount of light (number of photons) is the same in both cases but is spread over a sensor area which is 4 times larger in the full frame case , so the picture is darker and to adjust for this ISO has to be increased 4 times.
I want to understand this so please reply. All the best.
Thank you so much! Very well explained!!